idag har vi haft om eksponentiel sammenhæng.
som har formlen y=b*a^2 

man anvender eksponentiel sammenhænge når man skal finde ud af noget med:

• Befolkningsvækst,

• Bakterievækst.

• Rentes rente (f.eks. når man her penge i banken)
• Radioaktivitet (halveringstid)
• Opvarmning og afkøling 

grafen kan se sådan her ud. 

A kan både hedde grundtal og fremskrivningsfaktor.

B er skæring med y-aksen

vi har også kort lært om kvanter: 

Potentiel funktioner

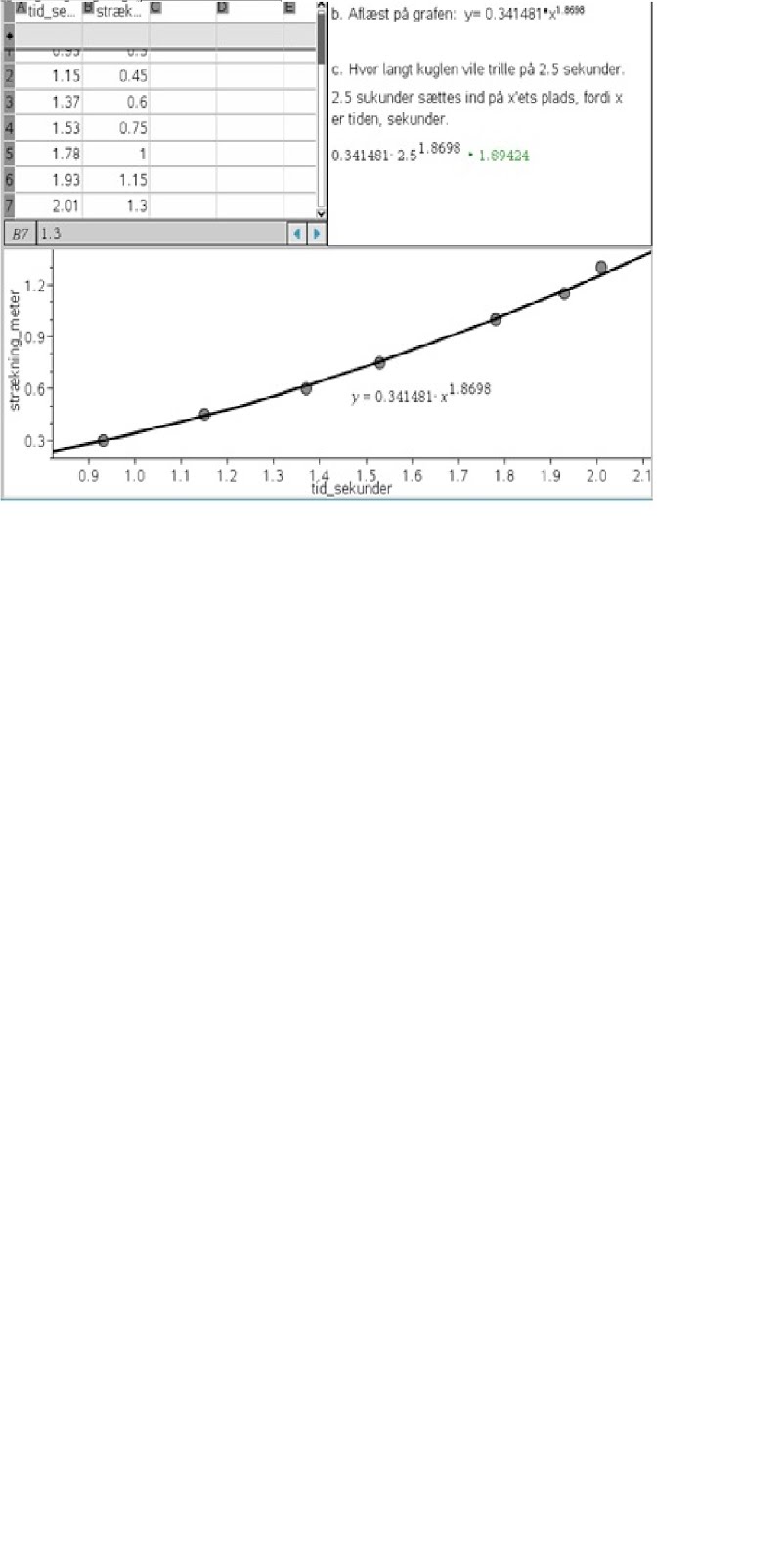
Vi tog hul på den første etape af potentiel sammenhænge.

Den går ud på anvendelse og praktiske informationer. F.eks. hvordan ser grafen ud visuelt?

Når man  har en formel kan man forudsige ting.

center;"> y=365*x^149933

Vi lavede en opgave:

En rumsonde bliver sendt i kredsløb omkring solen.

Afstanden til solen er 450 millioner km.

Hvor lan tid tager et omløb?

Først skal vi have styr på benævnelserne. I dette tilfælde er x astronomisk afstand og y er tid i sek.

Vi bruger astronomisk enhed som afstand. 1 astronomisk enhed er afstanden fra solen til jorden.

Vi kender jordens afstand til solen. Den er 149 millioner km. Så skal vi omregne rumsondens afstand til solen om til astronomisk enhed.

450/149 = ca. 3.

Nu har vi vores x, og så sætter vi det ind på x'ets plads.

 

y=365*3^149933 = 1896 dage

1896 dage / 365 dage = 5 år ca.

 

Vi lavede ligeledes opgave 22 på side 32 i bogen.

 

 

Matematik med Leif

Vi startede med at klippe kvadrater og cirkler ud. Derefter skulle vi veje dem.
Da vi havde vejet dem skrev vi dem ind i et regneark i Ti-Nspire, med vægt og diameter/sidelængde.
Så skulle vi snakke om sammenhængen mellem længden og massen. Da vi skulle snakke om det, lavede vi et diagram over det i Ti-Nspire, så vi nemmere kunne se sammenhængen.


Kvadrat:
y = 0,018011*x^2,00498

potentiel funktion

y = b*x^a

Areal: X^2
X=sidelængden

Cirkel:
y = 0,017011*X^1,9281

Areal: pi*r^2


Lineær: y = ax+b
potentiel: y=b*x^a
Eksponentiel: y=a^x